4. 탐욕법 (Greedy Algorithm)
분할 통치법은 알고리즘의 전략으로서는 약간 특이한 것으로서 이것은 상황이 잘 파악된 부분을 넓혀감으로써 서서히 해답에 가까워진다는 방식이다. 이런 방식에서는 해답에 접근해 가는 방법에 따라 능률이 좋아지기도 하고 나빠지기도 한다. 예를들면 선형 탐색과 2진 탐색은 목표로 하는 레코드에 어떻게 접근할 것인가가 다르기 때문에 효율에 큰 차이가 생기는데, 선형 탐색에서는 레코드에 한 발씩 접근하고, 2 진 탐색에서는 n / 2, n / 4, n / 8, … 의 폭으로 대담하게 접근한다.
해답에 접근하는 방법은 문제마다 여러 가지가 있는데 이들을 분류하는 것은 어렵지만 일반적인 전략도 많이 알려져 있다. 탐욕법 (greedy algorithm) 은 그중에서 가장 단순한 것으로 현재의 상황에서 국소적으로 보아 가장 좋은 경우를 택해서 나아가는데, 그외의 경우를 무시함으로써 능률의 향상을 기대할 수 있다. 예를들면 앞에서 설명한 Dijkstra 알고리즘과 Prim 알고리즘은 현재 갖고 있는 지식을 이용해서 길이가 가장 짧은 경로 또는 변을 택하기 때문에 탐욕법의 알고리즘으로 분류된다.
탐욕법의 본질적인 문제점은 국소적인 관점에서 가장 좋은 선택이 대국적인 관점에서 보았을 때도 좋은 선택이라는 보증이 없다는 것이다. 즉 눈앞의 이익에 급급해서 큰 이익을 놓칠 우려가 있다. 그러나 문제에 따라서는 국소적인 최선과 대국적인 최선이 일치하는 경우가 있는데 그러한 경우에는 매우 유효한 기법이다. 위에서 설명한 두 가지 알고리즘이 경우 대국적인 최적해를 이 방법으로 구할 수 있다는 것은 각각 이미 증명된 대로이다.
탐욕법에서는 항상 대국적인 관점에서는 최적해를 얻을 수 있다고는 할 수 없는데, 인생과 마찬가지로 「욕심」이란 지금 당장은 좋은 결과를 얻을지 모르나 전체로서는 나쁜 결과를 초래할지도 모른다. 예로서 Dijkstra 알고리즘과 Kruskal 알고리즘에서 변의 무게가 음인 경우가 있을 때는 어떻게 되는지를 상기해 보자. 음의 무게를 가진 변이 존재하는 경우에는 Kruskal 의 최소목 알고리즘에는 영향이 없으므로 최소목을 제대로 구할 수 있지만, Dijkstra 알고리즘은 경우에 따라 최단 경로를 구하지 못하는 경우가 있다.
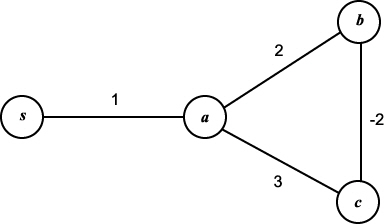
그림 12 음의 무게를 가진 그래프
예를들어 그림 12 와 같은 그래프에서는 b 와 c 사이에 음의 무게를 가진 변이 있다. 출발점을 s 로 해서 Dijkstra 알고리즘을 적용하면 우선 a 까지의 길이가 1 인 최단 경로를 구하게 된다. 다음은 s 와 a 에서 b 와 c 로 향하는 변만을 조사하므로 b 가 s 에 가장 가깝다고 생각한다. 이 「최단 경로」는 s → a → b 로 길이는 3 이다. 그 후에 s 에서 c 로의 최단 경로의 길이가 1 이라는 것을 알게 된다.
그러나 c 를 택하기 전에 b 를 선택한 「욕심많은」선택은 넓은 시야에서 보면 잘못된 것이다. s → a → c → b 라는 경로의 길이는 2 이므로 b 의 최단 거리가 3 이라는 것은 잘못되었다.
문제에 따라서는 최적해를 구하는 탐욕 알고리즘이 존재하지 않을지 모르지만 상당한 확률로 최적해에 가까운 답을 구하는 탐욕 알고리즘이 존재하는 경우가 있다. 대개는 최적해보다도 수 퍼센트 정도 코스트가 커도 관계없다. 이와 같은 경우 최적해에 가까운 답을 구하는 보다 빠른 방법이 탐욕 알고리즘이 되는 경우도 많다. 모든 경우를 조사하지 않으면 최적해가 구해지지 않는 문제라면 탐욕 알고리즘과 그외의 발견적인 방법을 사용해서 (최적해가 아닐지도 모르지만), 최적해에 가까운 답을 구하는 것이 보다 현실적이다.
최적해를 구하기 위해서는 모든 가능성을 조사해야 하는데, 그렇게 되면 입력의 크기를 지수로 하는 시간이 걸린다는 유명한 문제 (순회 세일즈맨 문제) 를 소개하기로 하자.
순회 세일즈맨 문제 (traveling salesman problem, 이후 「TSP」라고 한다) 란 변에 무게가 할당된 무방향 그래프에서 변의 할당된 무게의 합이 가장 적은 폐로 (모든 정점을 단 한번만 포함하는 폐로) 를 구하는 문제이다. 이러한 폐로를 해밀턴 폐로(hamilton cycle) 라고 한다.
그림 13 에 순회 세일즈맨 문제의 한 예를 나타냈는데 이 그래프에는 정점이 6개 있다. 각 정점의 좌표가 주어져 있으므로 변의 길이를 그 변의 무게라고 한다. TSP 에서는 일반적으로 대상이 되는 그래프를 모든 두 정점 사이에 변이 존재하는 완전 그래프라고 가정하는데, 변의 무게가 유클리드의 거리가 아닌 일반적인 경우에는 존재하지 않는 변은 무게가 무한 대라고 생각하면 된다.
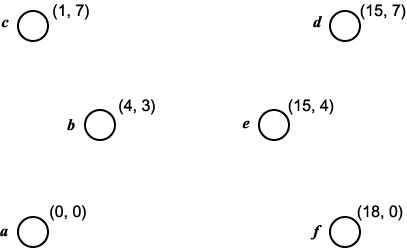
그림 13 순회 세일즈맨 문제의 예
그림 13 에 있는 6 도시를 순회하는 네 가지 폐로의 예를 그림 14 에 나타낸다. 그들 각 폐로의 길이는 52.13, 49.73, 48.39, 49.78 로 그림 6 ~ 14 에 나타낸 폐로 중에서 (c) 가 가장 짧다.
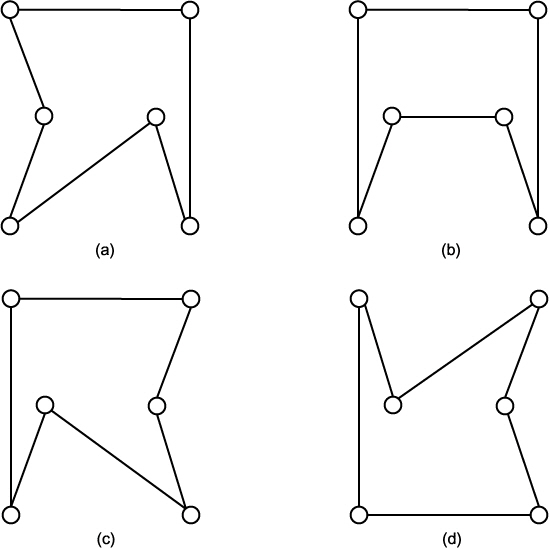
그림 14 폐로의 예
TSP 에는 실용적인 응용이 몇 가지 있는데, 이름이 나타내는 바와 같이 여러개의 지점을 방문하고 나서 출발점에 되돌아오는 코스를 정하는데 사용할 수 있다. 예를들면 우편 배달부가 다니는 코스는 TSP 를 사용해서 정할 수 있는데 이 경우 각 정점은 우체통의 장소를 나타내고 변의 코스트는 두 정점간의 이동 시간을 나타낸다.
TSP 에 대한 탐욕 알고리즘으로서는 kruskal 알고리즘의 변형을 생각할 수 있다. Kruskal 알고리즘과 마찬가지로 우선 가장 짧은 변을 선택한다. Kruskal 알고리즘에서는 선택하려는 변을 추가하더라도 폐로가 구성되지 않는 변을 하나씩 확정했다. TSP인 경우에는 선택하려는 변을 추가했을 때,
(1) 차수 (degree: 정점에 연결된 변의 수) 가 3 이상인 정점이 되지 않고,
(2) 폐로가 구성되지 않는 (단, 선택한 변의 수가 주어진 문제의 정점수와 같은 경우는 제외) 변을 확정한다.
위의 두 가지 조건을 이용해서 차례대로 변을 선택하면 서로 연결되어 있지 않은 경로가 여러 개 구성되고, 마지막 스텝에서 남은 하나의 경로가 닫혀서 폐로가 된다.
예를들면, 그림 13 에서는 변 (d, e) 가 길이 3 으로 가장 짧으므로 우선 이것을 선택한다. 다음은 길이가 5 인 변 (b, c), (a, b), (e, f) 를 조사하는데 이들의 순서는 아무래도 좋다. 세 개 다 조건을 만족하고 있으므로 탐욕 방법을 사용하면 세 개를 모두 확정해야 한다. 그리고 나서 남는 변 중에서 가장 짧은 것은 (a, c) 로 그 변의 길이는 7.08 이다. 그러나 변 (a, c) 는 (a, b) 및 (b, c) 와 함께 폐로를 형성하므로 확정할 수 없다. 마찬가지로 다음의 변 (d, f) 도 버린다. 다음에 변 (b, e) 를 조사하지만 이 변을 추가하면 b 와 e 의 치수가 3이 되어 버리므로 지금까지 선택한 변과 합해도 폐로가 되지 않기 때문에 확정할 수 없다. 마찬가지로 (b, d) 도 버린다. 다음에 (c, d) 를 선택하면 a → b → c → d → e → f 라는 하나의 경로가 구성되는데, 이 경로에 마지막으로 (a, f) 를 선택해서 추가하면 그림 15 와 같은 폐로가 완성된다.
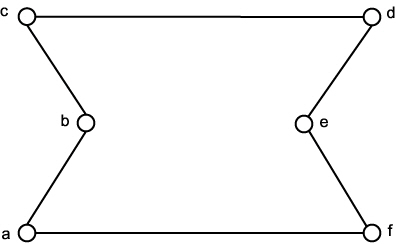
그림 15 순회 세일즈맨 문제의 답
