2. 균형법

2. 균형법


앞에서 설명한 분할 통치법의 예에서는 모두 원래의 문제를 크기가 같은 부분 문제로 분할했는데, 좋은 알고리즘을 설계하기 위한 기본적인 지침 중에 부분문제의 크기가 균등해야 한다는 것이 있다. 이것을 설명하기 위해서 정렬의 예를 사용해서 문제를 균형이 맞지 않는 크기를 가진 부분 문제로 분할한 결과와 같은 크기로 분할한 결과를 비교해 보자. 이 예에서 균형화가 유효하다는 것은 분할 통치법에만 한정된 것이라고 생각해서는 안된다.

n 개의 정수로 구성된 데이터를 크기가 적은 순으로 정렬하는 문제를 생각해 보자. 이 문제를 해결하기 위한 가장 단순한 정렬법은 데이터열을 앞에서부터 차례대로 조사해서 가장 작은 요소를 찾아낸 뒤, 제일 왼쪽에 있는 데이터와 교환하고, 그 다음에는 제일 왼쪽에 있는 데이터를 제외한 데이터열을 앞에서부터 차례대로 조사하여 가장 작은 요소를 찾아낸 뒤, 왼쪽에서 두 번째에 있는 데이터와 교환하는 것을 반복하는 것이다. 이 과정을 나머지 데이터에 대해서도 반복 적용함으로써 n 개의 데이터에 대한 정렬을 할 수 있다.

이 알고리즘에 의해 정렬되는 요소 사이에서 행해지는 비교 횟수를 평가해 보자. 제일 적은 데이터를 정하기 위해서는 n - 1 번 비교를 해야 하고, 두 번째 작은 데이터를 정하기 위해서는 n - 2 번, 그 다음 데이터를 정하기 위해서는 n - 3 번을 비교해야 한다. 전체 비교 횟수는 이들을 합하면 되므로,

        

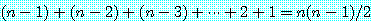
이 되어 O(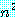) 이 된다.

이 정렬 알고리즘은 크기가 다른 부분 문제로 분할하는 분할 통치법을 재귀적으로 적용한 것이라고 볼 수가 있지만 크기 n에 대해서는 효율이 좋지 않으므로 오더상으로 효율이 좋은 정렬 알고리즘을 설계하기 위해서는 부분 문제의 크기를 균등화해야 한다. 크기가 n 인 문제를 크기 1 과 크기 n - 1 인 두 부분 문제로 분할하지 않고, 문제를 크기가 거의 반인 두 개의 문제로 분할해야 하는데, 이것은 앞에서 이미 설명한 합병 정렬이라는 정렬 알고리즘에서 이용되고 있다.

합병 정렬에 대해서는 이미 설명했으므로 알고리즘에 대한 설명은 생략하지만 이미 설명한 바와 같이 이 알고리즘의 복잡도는 O(n log n) 이다.

이와 같이 부분 문제의 크기를 균등하게 함으로써 훨씬 효율이 좋은 알고리즘을 만들 수 있게 된다.