Programming world

1. 분할 통치법(divide and conquer)


효율이 좋고 알고리즘을 설계하는 기법으로서 가장 널리 사용되고 있는 기법중에 분할 통치법 (divide-and-conquer) 이라는 것이 있는데, 분할 통치법에서는 해결하려고 하는 문제 (크기를 n 이라고 한다) 를 크기가 보다 작은 여러 개의 부분 문제로 분할한다. 단, 이 때 크기가 작은 부분 문제에 대한 답으로부터 원래의 문제에 대한 해답을 쉽게 얻을 수 있게 분할할 필요가 있다. 이 기법에 대해서는 합병 정렬과 2 진 탐색목 등 몇 가지 응용 예를 지금까지 살펴보았다.

우선 문제를 분할하면 어느 정도 효과가 있는지를 예를 통해 살펴보기로 하자.

탁구 대회를 열어서 가장 탁구를 잘 하는 사람과 가장 못하는 사람을 정하려고 한다. 실력이 좋은 사람이 항상 이긴다고 했을 때 몇 번 시합을 하면 되는가를 계산하는 것이 문제이다.

여기서 탁구 대회 참가 인원을 n 명이라고 하자. 이 문제를 해결하기 위해서 스포츠 경기시에 일반적으로 많이 이용하는 「토너먼트법」을 이용하는데, 첫 번째 토너먼트에서는 가장 강한 사람을 결정하고, 그 다음에는 나머지 n - 1명 중에서 마찬가지로 토너먼트법을 이용해서 가장 약한 사람을 정하는 방법을 이용하기로 하자 (그림 1). 그림 1 에서 굵은 선은 시합에서 이긴 사람을 나타내고, × 표시가 있는 것은 진 사람을 나타낸다.

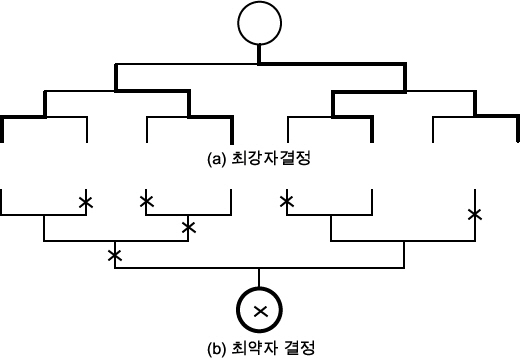
그림 1  탁구 대회

그림 1 과 같은 방법을 이용하는 경우에는 한번 시합을 할 때마다 한 사람씩 대상에서 제외되므로, n 명 중에서 가장 강한 사람을 정하기 위해서는 n - 1 번 시합을 하게 된다. 따라서 이 방법에서 필요한 시합수를 T₁ (n) 이라고 하면,

        

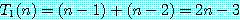
 이 된다.

그러나, 조금만 곰곰히 생각해 보면 그림 1 과 같은 방법을 이용하는 경우에는 불필요한 시합을 많이 한다는 것을 금방 알 수 있다. 첫 번째 토너먼트에서 이긴 사람 (약 n / 2 명) 은 자기가 이긴 상대보다는 강하다는 것은 알고 있으므로 다음 번에 실시하는 토너먼트에는 출전할 필요가 없다. 두 번째 토너먼트전은 첫 번째 토너먼트에서 한번도 이기지 못하고 진 사람만을 모아서 실시하면 되므로, 두 번째 토너먼트에 출전하는 사람수를 k 라고 하면 두 번째 토너먼트전을 운영하기 위해서는 k - 1 번 시합을 하면 된다.

이 방법으로 경기를 할 때의 시합수를 평가히가 위해서는 k 를 구해야 하는데, 이를 위해서는 첫 번째 토너먼트전을 구체적으로 어떻게 행하는지가 문제가 된다. 이 때 전년도 우승자에게 다른 사람이 차례로 한 사람씩 도전하는 방법을 택한다고 하고, 전년도 우승자가 모두에게 이기면 k 의 값은 n - 1 이 된다. 따라서, 이 방법을 이용하더라도 그림 1 의 방법과 같이 2n - 3 번 시합을 해야 한다 (그림 2).

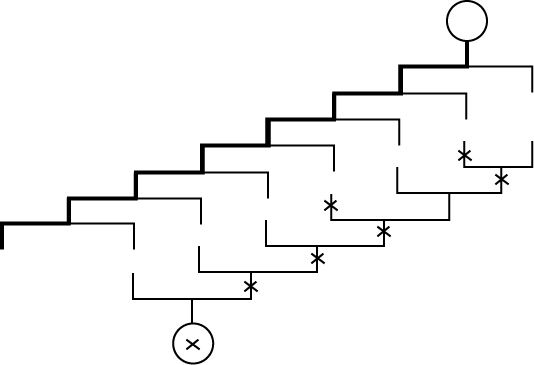
그림 2  비능률적인 경기 운영

그러나 n 명을 거의 반씩 나눠서 첫 번째 토너먼트를 하게 하면 k 의 값은 n / 2 이 된다 (그림 3).

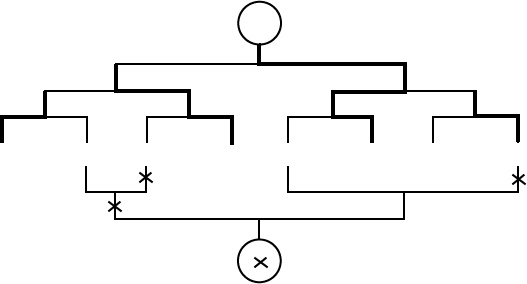
그림 3  능률이 좋은 경기 운영

이 때 계산을 간단하게 하기 위해 n을 짝수라 하고, 이 경우의 시합수를 T₂(n) 으로 하면,

        

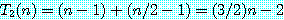
이 되어, 그림 1 의 방법보다도 n / 2 - 1 번이나 시합수가 적어진다.

그러면, 이번에는 또 다른 방법을 생각해 보기로 하자.

우선 전체를 반으로 나눠서 각 팀에서 따로따로 최강자와 최약자를 결정한 후, 양 팀의 최장자끼리 시합을 하게 해서 전체의 최강자를 정하고, 최약자끼리 시합을 하게 해서 최약자를 정하면 된다 (그림 4).

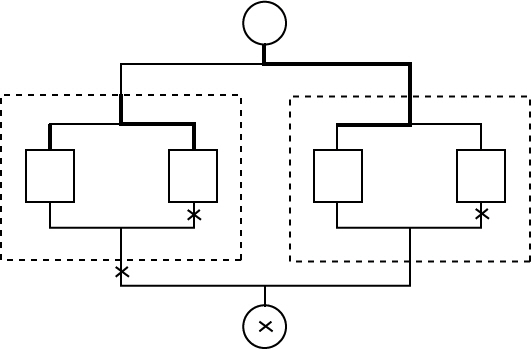
그림 4  분할에 의한 최강ㆍ최약자 결정

이 방법을 이용한 경우의 시합수를 T₃(n) 으로 하면,

        

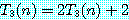
가 된다. 또, 분명히

        

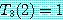
이다. 이 두 식을 이용하면 각 n 에 대해 다음과 같이 되는데, 계산을 간단하게 하기 위해 n = 2p 라고 한다.

        

        

        

        

        

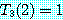
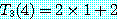
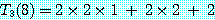
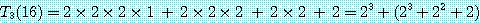
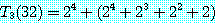
이것을 n 에 대한 일반식으로 나타내면,

       

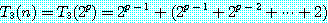
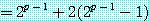
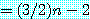
이 된다.

여기서 설명한 마지막 방법 (그림 4 의 방법) 에서는 우선 전체를 반으로 나눠서 (분할) 각각에 대해 원래와 같은 문제를 해결하고 마지막에 간단한 처리를 해서 전체에 대한 해답을 구한다 (통합). 이와 같이 전체를 분할해서 각각을 따로따로 처리하고 마지막에 통합하는 방법을 「분할 통치법」이라고 한다 (그림 5).

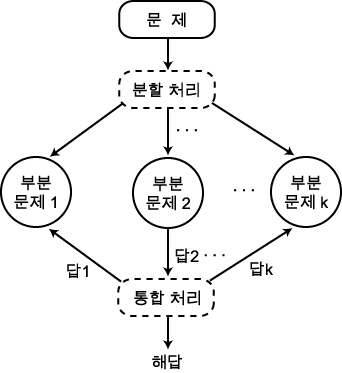
그림 5  분할 통치법의 원리

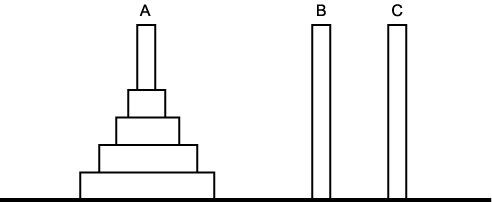
그림 6  하노이 탑 문제의 초기 상태

분할 통치법의 또 하나의 예로서 하노이의 탑이라는 게임을 생각하기로 하자.

그림 6 과 같이 세 개의 막대 A, B, C 가 있는데, 처음에는 A 라는 막대에 여러 개의 원판이 크기순으로 즉, 어떠한 원판을 보더라도 위에는 그보다 적은 원판이 있고 아래에는 그보다 큰 원판이 놓여져 있다. 이 게임의 목적은 원판을 막대에서 막대로 한번에 하나씩 이동해서 모든 원판을 막대 B 로 옮기는 것이다. 단, 어떠한 경우에도 적은 원판 위에는 큰 원판을 둘 수 없다.
이 게임은 다음과 같은 단순한 알고리즘으로 해결할 수 있다는 것을 알 수 있다. 막대가 삼각형의 형태로 배치되어 있다고 하고 홀수 번째에는 가장 작은 원판을 시계 방향으로 하나만 이동하고, 짝수 번째에는 제일 작은 원판을 제외한 나머지 원판 중에서 이동할 수 있는 것만을 하나 이동한다.
이 알고리즘은 간단하고 정당하지만 왜 정당한지를 금방 알기는 어렵지만 다음과 같은 분할 통치법을 이용하면 정당성도 금방 이해할 수 있을 것이다.

원판 n 장을 A 에서 B 로 이동하는 문제는 크기가 n - 1 인 두 개의 부분 문제로 구성된 것이라고 생각할 수 있다. 우선 n - 1장의 원판을 막대 A 에서 막대 C 로 옮기면 막대 A 에 있던 n 번째 작은 원판 (가장 큰 원판) 을 옮길 수 있는 상태가 되므로 그 원판을 A 에서 B 로 옮긴다.
그리고 나서, n - 1 장의 원판을 막대 C에서 B로 이동한다. n-1장의 원판을 옮기기 위해서는 이 방법을 재귀적으로 사용하면 되는데, 여기서 이동하는 n - 1 장의 원판은 다른 어느 원판보다도 작으므로 이동할 때에 막대 A, B, C 의 제일 윗부분에는 어떠한 원판이 있는지를 생각할 필요가 없다. 실제로 여러 개의 원판이 어떻게 이동하는지는 알기 어렵고, 재귀 호출이 반복되므로 이것을 하나하나 체크하기는 힘들지만, 이 알고리즘의 아이디어는 이해하기 쉽고 정당하다는 것을 증명하는 것도 비교적 쉽다. 일반적으로 이와 같은 분할 통치법을 이용한 알고리즘은 그렇지 않은 알고리즘보다 효율이 좋다.
분할 통치법을 이용해서 알고리즘을 설계할 때에는 문제를 분할하는 방법 및 각 부분 문제에 대한 답을 통합시키는 방법도 고려해야 한다. 특히 부분 문제의 답에서 전체의 문제에 대한 답이 비교적 간단하게 얻어지지 않으면 이 기법은 사용할 수 없는 것이라고 생각해야 한다. 문제의 분할법도 알고리즘의 성능에 영향을 미치기 때문에 중요한다, 대부분의 경우 가능한 균등한 크기로 분할하는 것이 바람직하다.

부분 문제를 해결하기 위해서는 같은 프로시저를 재귀적으로 호출하는 것이 간단하고, 이 재귀 호출은 데이터수가 1 이 될 때와 같이 문제의 답이 분명하게 되는 시점에서 종료하게 된다.