Programming world

5. 백트랙킹법 (backtracking)


어떤 문제의 최적해를 구하려고 하지만 모든 가능성을 조사하지 않고는 최적해를 얻을 수 없는 경우가 있다. 여기서는 모든 가능성을 조직적이고도 효율적으로 조사할 수 있는 기법인 백트랙킹법 (backtracking) 을 소개하기로 한다.

게임 목 (game tree) 과 식 변형 목 등을 완전한 나무의 형태로 만들어서 컴퓨터에 기억시킬 수는 없다. 예를들면, 장기라던가 바둑에서는 경우의 수가 너무 많아서 이들을 전부 기술해서 한꺼번에 컴퓨터에 기억시키는 것은 불가능하기 때문이다. 그러나, 이들 나무는 구조가 매우 규칙적이다. 즉, 하나의 정점 (정점은 경우, 수식, 논리식 등을 나타낸다) 에서 어느 정점으로 변이 접해 있는가가 여러 개의 규칙에 의해 명확하게 정해져 있으므로 나무를 만들어 가면서 조사를 할 수가 있다.
여기서는 백트랙킹을 설명하기 위해 3목이라는 게임을 이용하기로 한다. 3목이란 게임은 두 사람이 그림 16 과 같은 사각형에 바둑돌을 교대로 놓아서 세 개의 돌을 동일 직선상에 먼저 놓는 사람이 이기는 게임이다. 그림 16 에서 각 칸에 쓰여진 번호는 각 칸을 구별하기 위해서 붙여 놓은 식별자이다.

그림 16  3 목의 초기 상태

그림 16 과 같이 전혀 바둑돌이 없는 초기 상태에서 출발해서 게임의 진행 상황을 보기 위해 하나의 경로를 따라가 보자. 포석은 기계적으로 「각 칸에 할당된 번호가 적은 순」으로 비어 있는 곳에 교대로 흑과 백을 놓는다. 이 방법을 토대로 그림 17(a) 와 같이 혹은 제일 처음에 왼쪽 위에 돌을 두고, 백은 그 오른쪽 옆에 돌을 두어가면 일곱 번째에서 흑이 승리하게 된다.
이것은 하나의 시행 (trial) 에 지나지 않는다. 이렇게 하면 백이 패하게 되므로 백이 이길 수 있는 경우를 살펴보기 위해 백에 있어서 다른 방법을 모색해 보기로 하자. 이를 위해, 경우 E 로 「돌아와서」(이것을 백트랙 (backtrack) 이라고 한다) 다시 생각해 보면 그림 17(b) 와 같이 E 에서 F′ 로 나아갈 수가 있고, 이하 G′, H, I 로 진행하면 역시 흑이 이기게 된다.

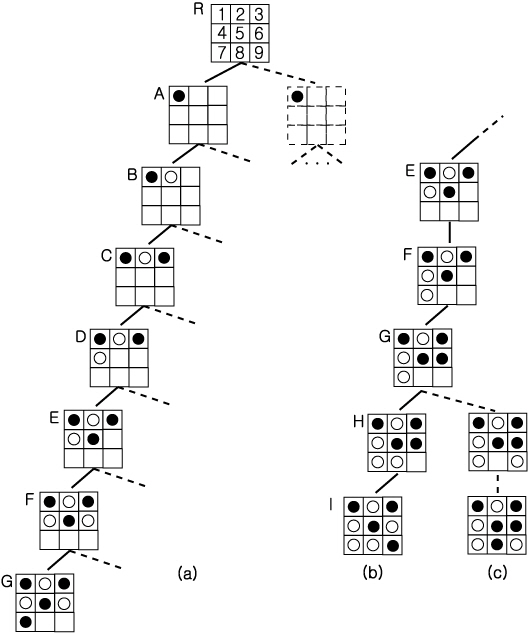
그림 17  시행과 수정

그러면 조금 더 백트랙해서 다시 보기로 하자. G′ 까지 백트랙하면 다른 경로를 발견하게 되는데 (그림 17 (c)), 그쪽 경로를 택해서 나아가면 비길 수 있다.

이러한 『시행과 수정』은 나무의 일부분만을 사용해서 행할 수 있는데, 이처럼 숨겨져서 표면에는 나타나지 않는 나무를 암목적 나무 (implicit tree) 라고도 한다. 암묵적 나무를 그림 18 과 같이 (일부분이긴 하지만) 보이게 그리면 시행과 수정 모습을 금방 알 수 있다. 그림 18 에서 아래로 향하는 변의 게임 진행을 나타내고, 위로 향하는 변은 백트랙을 나타내며, 점선은 지금 단계에서는 아직 조사되지 않는 경로를 나타낸다.

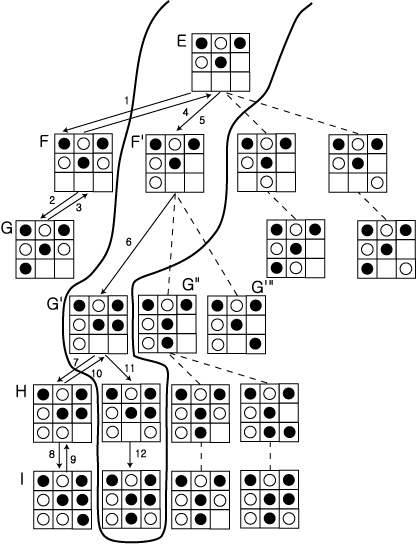
그림 18  E 를 루트로 하는 나무

그림 18 까지 행한 것은 나무상에서의 변을 번호순으로 늘리거나 줄이면서 (백트랙) 각 경우에 도달한 것이다. 여기까지의 단계에서 경우 F 에서는 흑이 승리하고, 경우 G′ 에서는 비긴다는 것을 알 수 있다. 이후 경우 F′에서는 누가 이기는가를 알아보기 위해 계속해서 백트랙과 시행을 계속하면 경우 E 에서는 흑이 승리한다는 것을 알게 되고, 최종적으로는 초기 상태 (그림 14 R) 에서는 비긴다는 것을 알게 될 것이다.

여기서 중요한 것은 하나의 경로를 조사할 때는 거기에 나타나는 경우만을 기억해 두면 된다는 것이다. 아직 고려하지 않은 경우와 이전에 고려의 대상이었지만 백트랙킹에 의해 현재의 경로에 포함되지 않는 경우는 잊어 버려도 된다. 이와 같이 함으로써 완전한 나무를 만들어 낼 때보다는 훨씬 적은 기억 용량으로 전체를 계속 조사할 수가 있다.

이러한 「조사」를 능률적으로 행하기 위해서는 조사하지 않아도 되는 부분을 조사 대상에서 제거하면 되는데, 조사 대상을 제거하는 기법으로 α - β 변 제거라는 것이 있으나 여기서는 생략하기로 한다.